The definition of depth of field and depth of focus in microscopy and how to calculate each one
An important concept in microscopy is the depth of field, and the depth of focus, which are two related principles that are often interchangeably used. Both of these things have to do with the range of distance where the image is clear and in focus.
The depth of field is inversely proportional to the numerical aperture of the objective lens, directly proportional to resolution, contrast, and working distance, and is also affected by magnification.
Below is a detailed explanation of what the depth of field and depth of focus are, the different factors that affect the depth of field, and how to calculate it.
What is depth of field in a microscope?

The depth of field is defined as the distance between the nearest and farthest object planes that are both in focus at any given moment. In microscopy, the depth of field is how far above and below the sample plane the objective lens and the specimen can be while remaining in perfect focus.
It is the axial or longitudinal resolving power of the objective lens, measured parallel to the optical axis. This number is largely determined by the numerical aperture of the objective lens, and is considerably small that it’s typically measured in microns.
Out of all natural and artificial optical instruments, the human eye has one of the best depth of field.
What is depth of focus?

While the depth of field refers to the object space, or the quality of the image coming from a stationary lens as the specimen is being repositioned, depth of focus talks about the image space, or the ability of the sensor to retain the focus of the image as the sensor changes positions.
It’s a somewhat more advanced and complex microscopy concept, since it takes into account the tilt and tip of the space between the image plane and the objective lens sensor plane. It’s also affected by aberrations and diffraction figures extending above and below the image plane.
The depth of focus is determined by both the numerical aperture or sensor size and the magnification of the objective lens, and is also, in a way, related to the resolution.
What factors affect the depth of field?
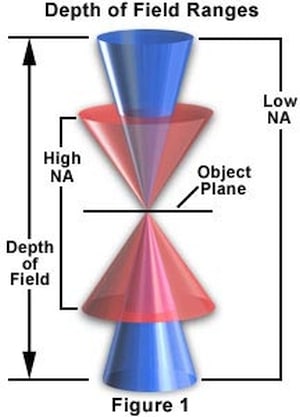
Knowing the depth of field of the microscope at any given setting is important since it affects how much you have to move the specimen slide up, down, left, or right to image certain areas of the specimen, especially since it determines the required stability of the focusing axis.
The numerical aperture of the objective lens is the main factor that determines the depth of field. In this sense, the microscope’s depth of field and depth of focus are somewhat similar, since these both generally increase as the numerical aperture is decreased.
Having said that, since the depth of field concerns the objective lens, there are a few other factors that must also be taken into account.
Numerical aperture
The general rule is that depth of field is inversely proportional to the numerical aperture, which is the size of the opening of an optical component where light passes through- in this case, the objective lens. So, a high numerical aperture results in a low depth of field, and vice versa.
With this in mind, the depth of field can be calculated by using this formula:
D = ( n² – NA²) / NA²
Where, d is the depth of field, λ is the wavelength of the light from the light source, n is the refractive index of the medium between the specimen and the objective lens, and NA is the numerical aperture of the objective lens.
Resolution
When it comes to image resolution or the clarity of detail of a specimen’s magnified image, this is typically inversely proportional to the numerical aperture, and therefore directly proportional to the depth of field.
So, we can say that at a low numerical aperture, both the resolution and the depth of field will be high, and so on.
This is because the distance between the angular resolution of the lens and the two intersecting points of the light path coming through the aperture are what determines the range of the depth of field.
Contrast
In relation to resolution is the contrast of the specimen and its magnified image. Different resolutions and contrasts have different corresponding depths of field. Smaller specimen details require a higher spatial frequency, and results in a smaller depth of field, while a lower contrast benefits from a higher depth of field.
Working distance
The working distance of the objective lens also has an effect on the depth of the field. A short working distance results in a smaller depth of field, while a longer working distance, as when focusing at the farthest point from the lens, creates a higher depth of field where almost everything before that point is in focus.
Magnification
In terms of magnification, this also has an influence on the depth of field of the microscope, especially when it comes to high magnification lenses, such as oil immersion lenses. Here, the depth of focus may be high, but the depth of field may below.
As such, there is a higher chance of making an error in focusing an image at higher magnifications, making the depth of field immensely important for thick and irregularly shaped objects with complex geometries or a variety of high and low surface points.
Meanwhile, for low magnification lenses and for infinitely thin specimens, focusing is not as much of an issue.
What is the best way to calculate the depth of field?
We have provided a general formula above for calculating the depth of field of the microscope, and this works perfectly well for low to average magnification lenses. But, there is actually another formula that is especially for high magnification optics.
This is because the two are governed by different principles, where the phenomenon of circles of confusion governs low magnification, and high magnification is governed by the principles of wave optics.
Hence, arguably the best way to calculate the depth of field is by combining both wave and geometrical optical depths of field.
D = (λ ⋅ n) / NA ² + ( n / (M ⋅ NA) ) e
Where d is the depth of field, λ is the wavelength of the illuminating light, n is the refractive index of the medium, NA is the numerical aperture of the objective lens, M is the lateral magnification of the lens, and e is the smallest resolvable distance of a detector on the image plane.
Average figures
- Light wavelength: More often than not, an optical microscope will make use of visible light to illuminate the specimen, which has a wavelength of 400 to 700 nanometers.
- Refractive index: Different mediums have different refractive indices. Air and vacuum both have an index of 1.00, water has 1.33, and immersion oil is at 1.52.
- Numerical aperture: The numerical aperture of the lens typically increases with the magnification, starting at around 0.25 on a 10x lens, then 0.6 to 0.8 on a 20x lens, and 1.47 on an oil immersion lens.
- Magnification: The magnification we are referring to is only that of the objective lens and not the ocular lens. For most light microscopes, this usually ranges from 4x to 100x.
The average depth of field at certain magnifications and apertures is 3 to 5 microns at 4x magnification, 0.5 microns at a 0.8 numerical aperture, and 0.1 to 0.2 microns at a 1.47 numerical aperture.
At this range, advanced auto-focus systems such as laser trackers are essential, since manual focusing is almost impossible to achieve.

